Public Problems and Model Solutions
Download our current public problems, their expert solutions, and model results in PDF format:
- Level 5 – One-Pole Problem
- Level 5 – Bias of a Sampled Halo Field
- Level 4 – SHO Vacuum Entanglement
- Level 4 – SUSY-Symmetry
- Level 3 – Slow-Roll Inflation
- Level 3 – Scalar Particle Scattering
- Level 2 – Dark Matter Capture as a Function of Time
- Level 2 – A 3-state QM Problem
- Level 1 – Blackbody in d Dimensions
- Level 1 – Boosted Parabolic Trajectory
Download the chain-of-thought report for DeepSeek-R1:
The model performance on public problems is as follows:
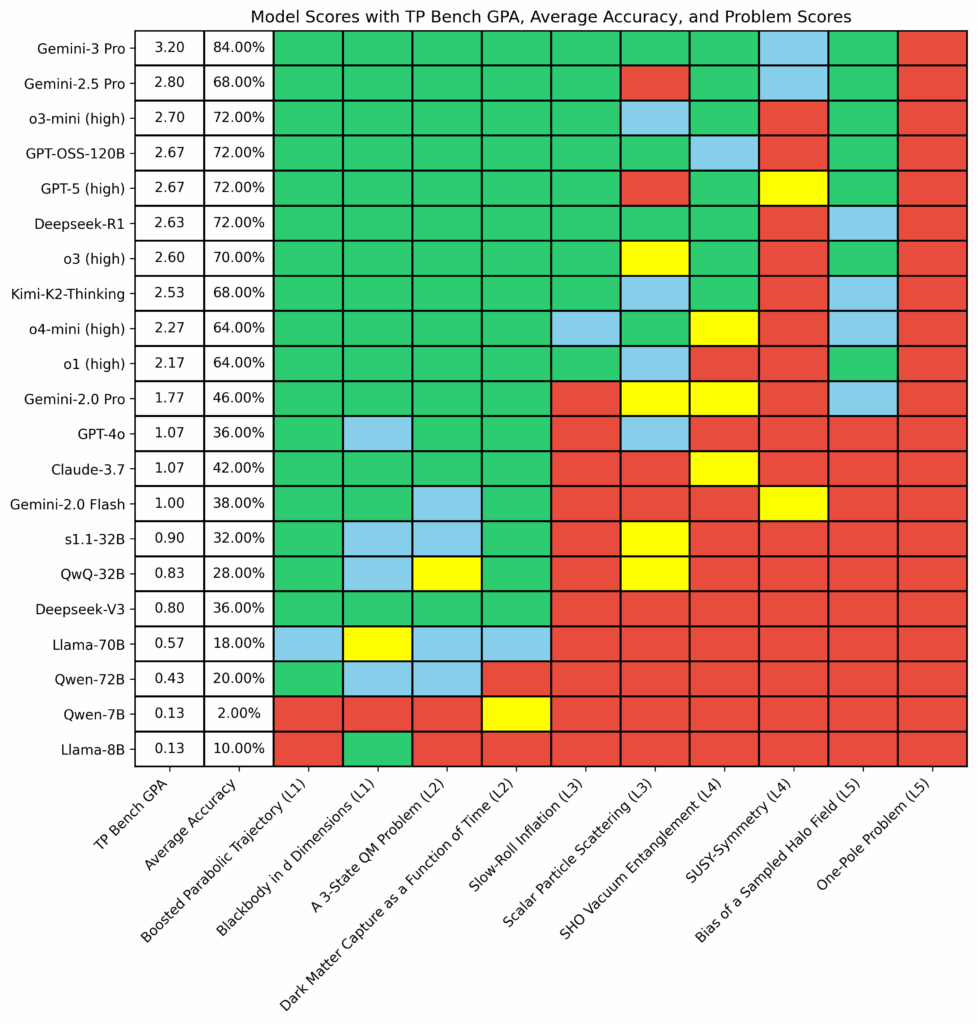
The meaning of colors in the plot:
- Green: Get the correct result for at least 4 out of 5 attempts
- Blue: Get 2-3 correct results out of 5 attempts
- Yellow: Get only 1 correct result out of 5 attempts
- Red: Fail to get correct result for all 5 attempts
The calculation method of TP Bench GPA:
Firstly, to each problem, we assign a numerical weight \(w\) from 1 to 5 based on its difficulty level. Next, we translate the color coding used above to assign a letter and a corresponding numerical grade \(g\) as follows:
(a) Green: Letter grade A which is assigned a numerical value of \(g=4\).
(b) Blue: Letter grade B and is assigned a value of \(g=3\).
(c) Yellow: Letter grade C and \(g=2\).
(d) Red: Letter grade F which is set to \(g=0\).
Finally, we apply the following formula to determine GPA (out of 4) \[ {\rm GPA}=\frac{\sum_{i=1}^{N}w_{i}\times g_{i}}{\sum_{i=1}^{N}w_{i}} \] where \(N\) represents the total number of attempts across all problems.
Looking ahead, we plan to improve and introduce additional evaluation metrics, one of which could incorporate confidence and precision to better capture the variability of model responses across multiple attempts on the same problem. This metric would impose penalties on models that exhibit high inconsistency in their responses, ensuring a more nuanced assessment of a model’s reliability and robustness. More intriguingly, as we enable models to learn and improve incrementally from their previous attempts, rather than treating each attempt as independent, we will need to develop more sophisticated metrics to evaluate their performance accurately.
